Pero comencemos con lo más básico. Comencemos con una una sucesión de números positivos
 . Para poder sumar esta cantidad infinita de términos, hay que ir poco a poco, así que vamos a ir sumando términos uno a uno y vamos a llamar suma parcial n-ésima a
. Para poder sumar esta cantidad infinita de términos, hay que ir poco a poco, así que vamos a ir sumando términos uno a uno y vamos a llamar suma parcial n-ésima a  . Así, obtenemos una nueva sucesión
. Así, obtenemos una nueva sucesión  de forma que cada término de esta está cada vez más cerca de la suma infinita
de forma que cada término de esta está cada vez más cerca de la suma infinita  , que es lo que se pretende conseguir, es decir, podemos decir que
, que es lo que se pretende conseguir, es decir, podemos decir que  . Así, un problema de sumas, lo convertimos, por arte de
. Así, un problema de sumas, lo convertimos, por arte de En fin, que, más o menos, tenemos las nociones básicas de cómo sumar una serie. Ahora vamos a entrar a definir (de forma poco o nada rigurosa) el concepto de serie telescópica. Éstas se caracterizan porque el término general
 puede escribirse, generalmente, como diferencia entre 2 términos (no necesariamente consecutivos) de otra sucesión, por ejemplo,
puede escribirse, generalmente, como diferencia entre 2 términos (no necesariamente consecutivos) de otra sucesión, por ejemplo,  para cierta otra sucesión
para cierta otra sucesión  . ¿Y por qué se llaman telescópicas? pues porque con esta estructura, es tremendamente fácil calcular el término general de la sucesión de sumas parciales:
. ¿Y por qué se llaman telescópicas? pues porque con esta estructura, es tremendamente fácil calcular el término general de la sucesión de sumas parciales: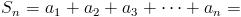
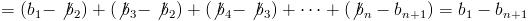
es decir, podemos cancelar la mayoría de los sumandos. Así, la convergencia de la serie
 dependerá exclusivamente de la convergencia de la sucesión
dependerá exclusivamente de la convergencia de la sucesión  .
.Por ejemplo, si queremos sumar
 , basta darse cuenta que
, basta darse cuenta que  , por lo que
, por lo que  , por lo que
, por lo que 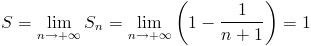
Realmente, en vez de un tipo específico de serie, se trata de una técnica de sumación, ya que se puede aplicar en otras situaciones. Por ejemplo, si es la diferencia entre 2 términos (no consecutivos)
 , o, incluso, si hay más de 2 términos como en el siguiente caso
, o, incluso, si hay más de 2 términos como en el siguiente caso  .
.Pero cuidado, que todo esto sólo vale si lo hacemos con las sumas parciales o, si lo hacemos con la suma infinita, si estamos seguros previamente de su convergencia, ya que en caso contrario podríamos llegar a falacias como la siguiente (visita Zurditorium si quieres ver otras falacias, incluida esta misma):
 .
.Finalmente, sólo quería comentaros que estas técnicas a veces hasta se usan en cosas importantes, como en una prueba de la que la suma de los recíprocos de los primos diverge (y por tanto debe haber una cantidad infinita de primos), en teoría del punto fijo o en teoría homológica.
En fin, espero no haberos aburrido mucho hoy.
Tito Eliatron Dixit Vota a Tito Eliatron Dixit en los Premios Bitacoras2010, categoría Ciencias

